

The projectile is thrown from beginning of cliff, which will be considered 78.4 m above the origin.īreak up velocity into X and Y components Starting position in X direction (X i) = 0 m Thrown horizontally = No vertical velocity (V i,y = 0) Y i = 0 m (see assumptions in first step) Replacing y f with Y mid, and t with t 1/2, Once again, it is recommended to break the projectile motion in half because that is where the maximum height is. This is our range.įinding the maximum height, we will use the second equation in the Y direction: The final position in the X direction is 31.249. Substituting V y,mid for V y, and t 1/2 for t,
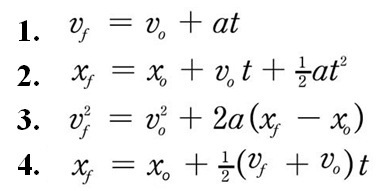
Since all the equations in the X direction have been used, transition to the Y direction.įor solving for the Y direction, it is recommended to split the projectile motion in half: Starting position in X and Y direction = 0 m (origin)ģ. Write down given information and make assumptions. How much time will it take for the ball to reach the ground and at what height will the ball be after each second of travel?ġ. A cannonball is launched horizontally from the top of a 78.4-meter high cliff at 10m/s. What is the horizontal range (maximum x above ground) of the object?Ģ. What is the total flight time (between launch and touching the ground) of the object?Ĭ. What is the maximum height reached by the object?ī. An object is launched at a velocity of 20 m/s in a direction making an angle of 25° upward with the horizontal.Ī. For the Y direction, it is recommended to split the projectile motion in half (when it applies – see General Notes above). Once you used all the equations for one direction, use the equations in the other direction.ī. There are some cases where you cannot solve for certain variables with one direction alone. Break up velocity into X and Y components.Ī. Make assumptions based on given information.Ģ. The max height is the maximum vertical displacement that the projectile reaches before falling back into the ground.īecause the acceleration in the X direction is zero and, the kinematic equations in the X and Y direction can be simplified:ġ. This is because when the ball reaches its highest point, it stops momentarily before reaching the ground. Velocity in the Y direction at the halfway point, or midpoint (V y, mid) is zero. It is negative because acceleration acts downward. Y direction:Īcceleration in the Y direction is. The range is the horizontal distance the projectile travels from the initial position to the final position. Since Vi, x is constant, acceleration in the X direction is Zero (a x= 0) Also, at the midpoint, velocity in the Y direction = 0 (see explanation below).
#Projectile motion equation full
That means at the half-way point, the time is also half of the full time (t 1/2). In cases where the projectile is thrown across a level ground (not thrown from a cliff or thrown to a higher ground), the situation can be split in half. Since it is thrown at an angle, the velocity must be broken up into components. The kinematic equations for each direction are displayed below:īelow are guidelines to keep in mind when solving projectile motion problems. The same kinematic equations apply, except that the X direction and the Y direction have to be solved separately. Think of a football player throwing a football, a soccer player kicking a soccer ball, or a golfer hitting a golf ball in the air.īecause the object is moving at an angle, the motion must be broken up into its X and Y components.
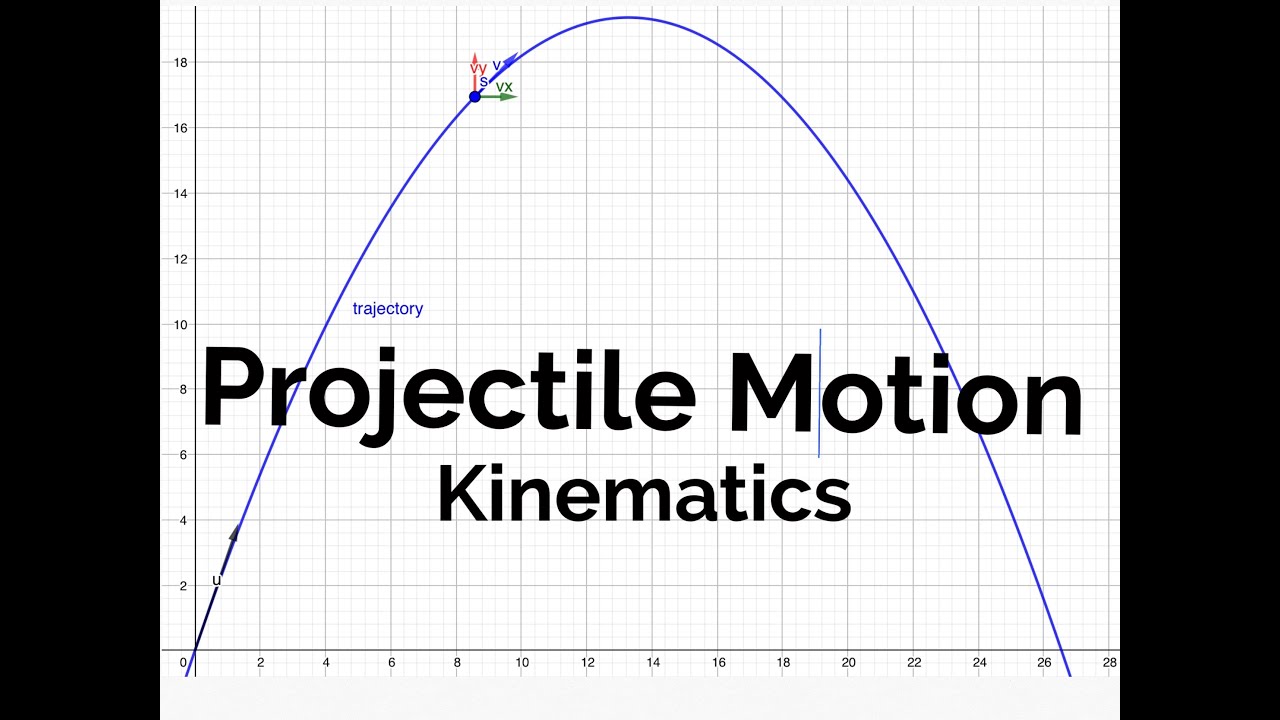
Projectile motion is when an object is thrown in the air at an angle.


 0 kommentar(er)
0 kommentar(er)
